Lab 5 - Algorytm poszukiwania ścieżki - A-star


Metody i algorytmy planowania ruchu - laboratorium
Lab 5 - Algorytm poszukiwania ścieżki - A*

1. Wprowadzenie
Celem zajęć jest zapoznanie się z jednym z podstawowych algorytmów poszukiwania ścieżki łączącej 2 wierzchołki w grafie. W naszych rozważaniach skupimy się, podobnie jak na poprzednich zajęciach na grafie w postaci siatki (zob. poniższy rysunek).
![]()
Na czarno zaznaczono komórki macierzy mapy, natomiast na niebiesko i zielono, odpowiednio wierzchołki i krawędzie odpowiadającego jej grafu.
Na poprzednich zajęciach poznaliśmy 2 algorytmy przeszukiwania DFS i BFS, które w rezultacie również umożliwiały poznanie ścieżki łączącej wyróżnione wierzchołki grafu. Jednakże, jak pewnie sami zauważyliście algorytmy te bardziej skupiały się na systematycznym przeszukaniu grafu, a nie na wyznaczeniu tej ścieżki. Znamienne jest, że nie korzystały one z bardzo istotnej informacji o położeniu punktu docelowego w procesie przeszukiwania grafu, czego skutkiem było odwiedzanie stosunkowo dużej liczby wierzchołków, które niekoniecznie zbliżały algorytm do celu. W dzisiejszym ćwiczeniu poznacie prostą metodę, która wykorzystując informację o położeniu celu przyspieszy znacznie proces odkrywania ścieżki łączącej wyróżnione punkty.
⚠️ Pamiętaj, aby w każdym nowym terminalu zanim rozpoczniesz pracę skonfigurować środowisko ROS komendą
source /opt/ros/humble/setup.bashlubsource install/setup.bash
2. Przygotowanie paczki w ROS
Zainstaluj paczkę ros-humble-nav2-map-server:
sudo apt-get install ros-humble-nav2-map-server ros-humble-nav2-lifecycle-managerPobierz paczkę z zadaniami z repozytorium github:
cd ~/ros2_ws/src
git clone https://github.com/BartlomiejKulecki/mapr_5_student.gitNastępnie skompiluj pobraną paczkę i odśwież przestrzeń roboczą:
cd ~/ros2_ws
colcon build --symlink-install
source install/setup.bashPliki points.py oraz grid_map.py są identyczne z tymi, które mieliście do dyspozycji na poprzednich zajęciach.
3. Algorytm A*
Algorytm A* należy zaimplementować w pliku
astar.py w polu oznaczonym komentarzami
(zawierają one przydatne informacje dotyczące dostępnych metod). Uwaga,
należy zaimplementować 2 metody search() oraz
heuristics(pos).
Metoda heuristics(pos) powinna zwracać odległość pozycji
pos do punktu końcowego. Przez odległość będziemy rozumieć
odległość Manhattan (\(L_1\)),
zdefiniowaną jako:
\[d(p, q) = |p_x - q_x| + |p_y - q_y|\]
gdzie \(p\) i \(q\) są wierzchołkami grafu, a \(p_x\) i \(p_y\) oznaczają współrzędne wierzchołka \(p\).
🔨 Zadanie 3.1
Wypełnij metody heuristics() oraz search()
klasy ASTAR tak aby realizowała algorytm A*, biorąc pod
uwagę, że niektóre komórki są zajęte (wartość komórki ustawiona na 100 -
reprezentują przeszkody, których nie należy odwiedzać), publikując co
krok mapę zajętości (odwiedzone komórki oznaczaj wartością 50) i
wyświetlając w konsoli informację o znalezieniu wierzchołka końcowego po
jego odwiedzeniu. Wyznacz ścieżkę łączącą początkowy wierzchołek z
wierzchołkiem celu odkrytą przez algorytm (lista tupli z indeksami
poszczególnych komórek). Na koniec działania algorytmu wyświetl tę
ścieżkę, korzystając z metody publish_path(path).
Kod uruchamia się poleceniem:
ros2 launch mapr_5_student astar_launch.pySpodziewany efekt (szybkość aktualizacji mapy zależy od argumentu
delay metody publish_visited):
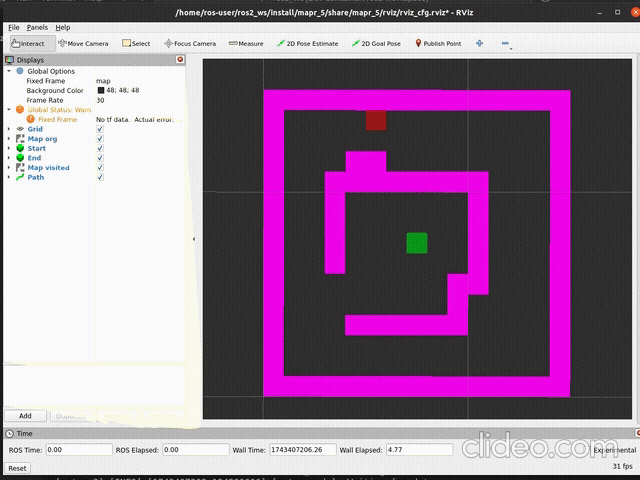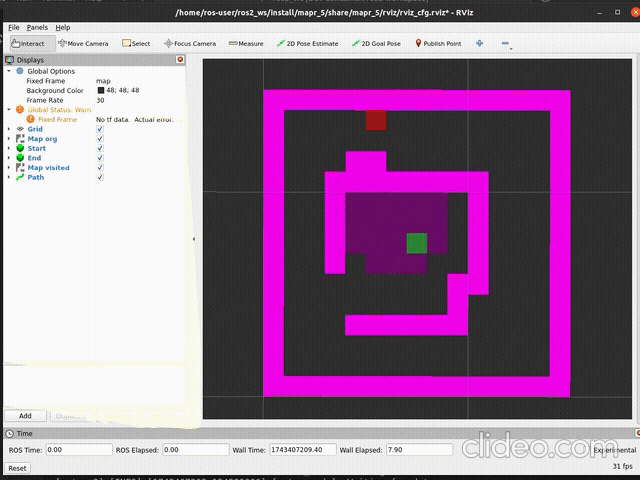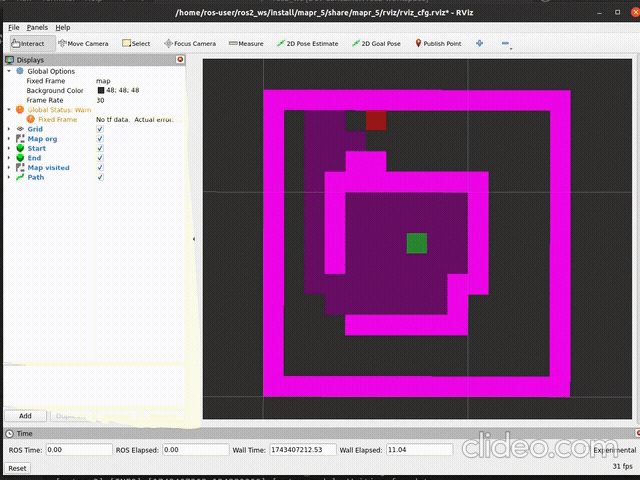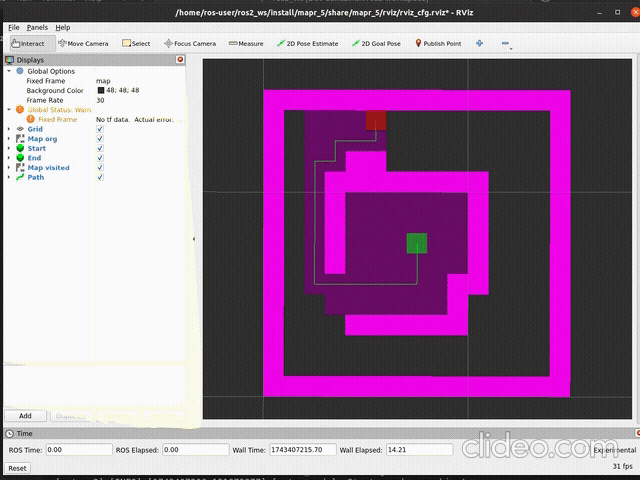 |
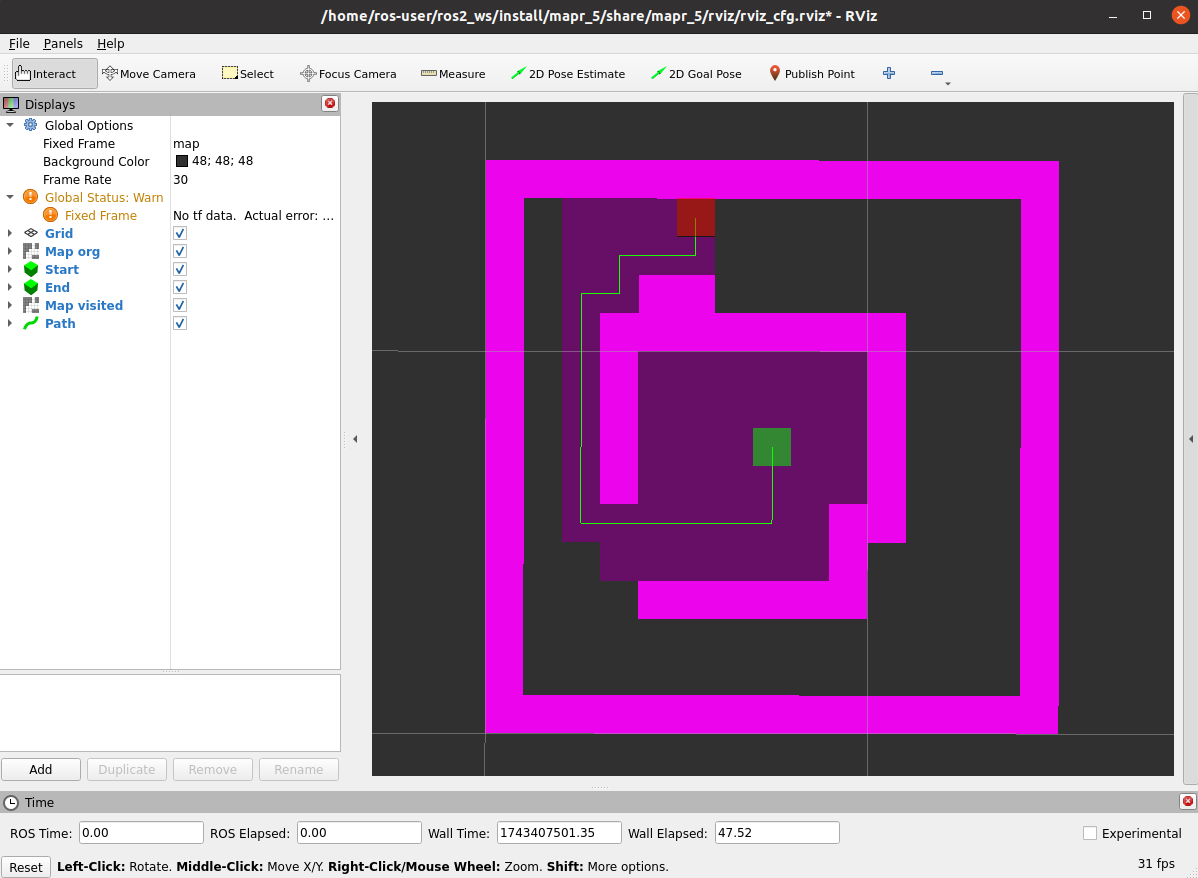 |
|---|---|
| działanie | stan końcowy |
Wskazówka 1 - pseudokod
I. Zainicjalizuj pomocnicze struktury danych.
II. Dodaj wierzchołek początkowy do zbioru wierzchołków do odwiedzenia.
III. Dopóki zbiór wierzchołków do odwiedzenia nie jest pusty:
A. Wyjmij wierzchołek ze zbioru, dla którego suma: odległości od startu do tego wierzchołka (po wyznaczonej ścieżce) oraz heurystyki, jest najmniejsza.
B. Sprawdź, czy ten wierzchołek jest wierzchołkiem końcowym, jeśli tak to zakończ algorytm i wyświetl ścieżkę.
C. Jeśli nie, to:
1. Zaznacz ten wierzchołek jako odwiedzony.
2. Dla każdego z jego sąsiadów (który nie jest ścianą) sprawdź, czy długość ścieżki od startu do tego sąsiada, przez aktualnie rozważany wierzchołek, jest krótsza niż dotychczasowa najkrótsza odległość od startu do tego sąsiada.
3. Jeśli tak (ad. warunek 2.), to:
a) Ustaw aktualnie rozważany wierzchołek jako rodzica tego sąsiada.
b) Ustaw dotychczasową najkrótszą odległość od startu do tego sąsiada jako dotychczasową najkrótszą odległość od startu do aktualnie rozważanego wierzchołka + koszt przejścia pomiędzy tymi wierzchołkami (domyślnie 1).
c) Dodaj do zbioru wierzchołków do odwiedzenia tego sąsiada.
Wskazówka 2
Jakość działania algorytmu silnie zależy od sposobu implementacji zbioru wierzchołków do odwiedzenia i metody wyszukiwania wierzchołka z najmniejszą wartością sumy heurystyki i odległości od startu.
Aby uzyskać szybki \(O(1)\) algorytm
wybierania najmniejszego elementu, można zastosować strukturę kolejki
priorytetowej, która w Pythonie jest dostępna w bibliotece
heapq:
https://docs.python.org/3.9/library/heapq.html.
🔨 Zadanie 3.2
Zmień w heurystyce odległość Manhattan (\(L_1\)) na odległość Euklidesową (\(L_2\)).
Spodziewany efekt (zwróć uwagę na przeszukane wierzchołki grafu - mapy):
![]()
🔨 Zadanie 3.3
Zmień w heurystyce odległość Manhattan (\(L_1\)) na odległość Czebyszewa (\(L_{\infty}\)).
Spodziewany efekt (zwróć uwagę na przeszukane wierzchołki grafu - mapy):
![]()
🔨 Zadanie 3.4 (dla chętnych 💪)
Jeśli chcesz poćwiczyć swoje umiejętności algorytmiczne zaimplementuj
strukturę danych min-heap samodzielnie, a następnie
wykorzystaj ją w swoim algorytmie.
Bardzo dobre wyjaśnienie sposobu implementacji tej struktury znajduje się w poniższym filmie: https://www.youtube.com/watch?v=B7hVxCmfPtM
Cała seria wykładów: https://www.youtube.com/watch?v=HtSuA80QTyo&list=PLUl4u3cNGP61Oq3tWYp6V_F-5jb5L2iHb
Myślenie algorytmiczne oraz znajomość podstaw algorytmów i struktur danych jest bardzo przydatna przy implementacji algorytmów planowania ruchu i pomaga zredukować czas ich działania.